ergo-log.com

Definition: "An ergogenic aid is any substance or phenomenon that enhances performance "

06.02.2011

Give endurance athletes 5 g taurine every day for a week...

...And very little happens. At least not in the Canadian study published in 2008 in the Journal of Applied Physiology. If taurine supplements boost endurance athletes' performance at all, the effect is minimal.

Taurine [structural formula shown here] is believed to enhance the effect of adrenalin in the body by increasing the number of adrenalin receptors in the body. That's the theory, at least. And although there’s no hard evidence to back up the theory, almost every energy drink contains not only the stimulant caffeine but also taurine.

Animal studies in which rats were given half a gram per kg bodyweight for two weeks revealed that the supplement increased the amount of time the animals were able to run in an exercise mill. [J Orthop Sci 2003;8(3):415-9.]

The Canadians were curious to know whether taurine has the same effect in humans, so they did an experiment with 8 endurance athletes. The athletes were given a 1.7 g dose of taurine 3 times a day for a week. At the end of the week the athletes had to cycle for 2 hours at 60 percent of their VO2max. That's a level at which it's just possible to keep up a conversation. The researchers also did the same test after the subjects had taken a placebo for a week.

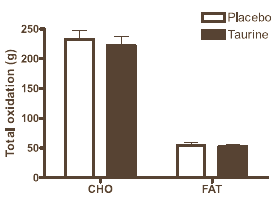
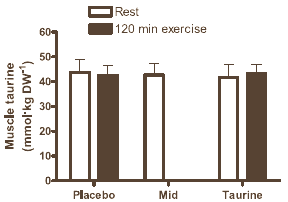
The supplement had no effect on the kind of fuel that the muscle cells used. Nor did the supplement change the ratio between the amount of carbs and fats that the muscle cells burnt. That's not so strange, because the muscle cells didn't absorb more taurine after taking the supplement. The concentration of taurine in the blood rose, but apparently taurine was not absorbed by the muscle cells.

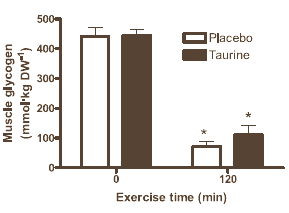
Nevertheless, the taurine supplement did have some effect. The levels of some amino acids did rise in the muscle cells – those of glutamine and the BCAAs valine, leucine and isoleucine all went up. Immediately after the exertion test, the glycogen concentration was slightly higher when the athletes had taken taurine. One explanation may be that the amino acids of which taurine raises the concentration function as glycogen precursors.

How taurine boosts the amino acid concentration the researchers dont know. One possibility is that taurine sabotages the build up of muscle proteins. If this is the case, athletes are better off not using taurine. Another possibility is that taurine boosts amino acid transport – in which case taurine might have an ergogenic effect. A small ergogenic effect.

Source:
J Appl Physiol. 2008 Aug;105(2):643-51.

More:
Animal study: taurine improves endurance 25.11.2008